Bitlerin, klasik bilgisayarların bilgiyi saklamak ve işlemek için kullandığı temel birimler olduğunu artık biliyorsunuz, ve bitler yalnızca tek bir değer alabilirler: 0 ya da 1. Ama bitler hangi değerleri alabileceklerini nasıl biliyorlar?
Talimatlar vererek bitlere ne yapacaklarını söylüyoruz. Bilgisayar kullanırken, aslında bitleri kontrol eden ve herhangi bir anda 0 mı yoksa 1 mi olacaklarını belirleyen, temel hesaplama bileşenlerine kadar uzanan talimatlar veriyoruz.
Arkadaşınıza “Mutlu yıllar!” yazan bir mesaj gönderdiğinizi varsayalım. Mesajlaşma uygulamanızı açıyorsunuz, her bir harfi tek tek yazıyorsunuz ve göndere basıyorsunuz. Her bir adım cihazınıza talimat vererek gerçekleşiyor. Bunlar sizin anlayabildiğiniz yüksek-seviyeli talimatlar, tıpkı ‘h yaz’ ya da ‘göndere bas’ gibi. Ama hesaplama cihazınız her bir talimatı makine-seviyesinde talimatlara bölüyor, ve en temel seviyede bu talimatlar, bit dizilerini kontrol ve manipüle ediyor.
Bu talimatlar bitler üzerinde işlemler yapan mantık kapıları ile gerçekleştiriliyor. Farklı kapılar, her biri özel bir işlem gerçekleştirmek üzere bir veya birden fazla bit üzerinde çalışabiliyorlar. Birleştirildiklerinde, sizin istediğiniz sonucu üretmiş oluyorlar.
Benzer şekilde, kuantum hesaplamada, kübitler üzerinde çalışan kuantum kapıları mevcut.
Kuantum Kapıları
Kuantum kapıları bizim kübitleri kontrol etmemize yarıyor - kübitlerdeki kuantum durumlarını manipüle ediyorlar. Bu da kübitler ölçüldüğünde elde edeceğiniz sonuçların olasılıklarını değiştirmek anlamına geliyor.
Bıyıkkent bilyesi benzetmesinde bir kuantum kapısı, bilyeye doğrudan bakıldığında kırmızı veya mavi görme olasılığını değiştiriyor.
Kuantum Devreleri
Talimatlar kuantum devreleri kullanılarak yazılabilir. Bir kuantum devresi kübitler üzerinde gerçekleştirilen kuantum kapılarının, ölçümlerin ve diğer eylemlerin sırasını gösteren bir modeldir. Gerçek fiziksel bir devre olmadığı halde, kübitlerin nasıl manipüle edileceğini gösterir.
Burada üç kübitli bir kuantum devresinin nasıl göründüğü ile ilgili bir örneği görebilirsiniz:

Bir nevi müzik notasını andırıyor, değil mi? Kağıttaki notalar gibi, devreyi de soldan sağa okuyoruz. Her yatay çizgi bir kübiti temsil ediyor. Bu çizgilerin üzerindeki kutular ve semboller kuantum kapıları, ve her bir çizginin sonundaki gri kutu ölçümü temsil ediyor. Bazı kuantum kapıları birden fazla çizgide bulunuyor - bu kapılar tek seferde birden fazla kübit üzerinde çalışan kapılardır.
Hatırlayın, bu kuantum kapısı sadece talimatların bir görsel temsili. Fiziksel donanımda gerçekleşeceklerin bir soyutlaması olarak düşünün; gerçek elektrik devrelerinin bir diyagramı gibi değil. Bu talimatlar bir *kuantum algoritması oluşturuyor.
Bıyıkkent’te, kediler müzik ile kuantum kapılarını dizilere uygular, bilyelerin durumlarını manipüle ederler. Belirli müzik notalarının bilyeler üzerinde belirli değişikliklere sebep olacağını bilirler.
Kuantum kapıları ve devreleri üzerinde daha fazla bilgi edinmek için okumaya devam edin! İstemiyorsanız, diğer bölüme geçebilirsiniz: Bu Son Değil.
Kuantum Kapılarının Matematiksel Gösterimleri
- bölümde, keyfi bir kübit durumunu göstermek için bu denklemi kullandığımızı öğrendiniz:
$\alpha_{0}$ ve $\alpha_{1}$ olasılık genlikleri olmak üzere, \begin{equation} \ket{\psi}=\alpha_{0}\ket{0}+\alpha_{1}\ket{1} \end{equation}
Bu olasılık genlikleri bize kübitin durumu hakkındaki her şeyi söylerler. Bir kuantum kapısı durumu değiştirdiğinde, $\alpha$ (‘alfa’ diye okunur) değerlerini değiştirir.
Kuantum kapımıza $G$ diyelim. $G$’yi başlangıç durumumuza $\ket{\psi}$ uygularsak, durum bu şekilde değişir:
\begin{equation} \alpha_{0}\ket{0}+\alpha_{1}\ket{1} \rightarrow \beta_{0}\ket{0}+\beta_{1}\ket{1} \end{equation}
Yeni $\beta$ değerleri (‘beta’ diye okunur) son durumumuzun olasılık genlikleridir.
Eğer biraz lineer cebir biliyorsanız kuantum durumlarını ve kapılarını göstermeye yardımcı başka bir yol daha vardır. Olasılık genliklerini sütun sayıları ya da sütun vektörleri ile şu şekilde de yazabiliriz:
\begin{equation} v_\psi = \begin{bmatrix} \alpha_0 \\ \alpha_1 \end{bmatrix} \end{equation}
Bu vektöre durum vektörü denilir. Benzer şekilde, herhangi tek-kübitlik bir kuantum kapısını da küçük bir sayı tablosu olarak yazabiliriz ($2 \times 2$’lik bir matris):
\begin{equation} G = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \end{equation}
Sonrasında da sonuçlanan durumu elde etmek için standart matris çarpımını kullanabiliriz: \begin{equation} \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} \alpha_0 \\ \alpha_1 \end{bmatrix} = \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} \end{equation}
Hadi şimdi yaygın olarak kullanılan iki örneği inceleyelim!
DEĞİL(NOT) Kapısı
Kuantum DEĞİL kapısı klasik kuzenine oldukça benzerdir. Klasik hesaplamada, bir DEĞİL kapısı 0 olan bir biti 1’e ya da 1 olan bir biti 0’a çevirir. Kuantum versiyonu da benzer bir şey yapar - $\ket{0}$ ve $\ket{1}$’in olasılık genliklerini yer değiştirir. Bu, kübitiniz ölçüldüğünde size 0 verme olasılığı daha yüksekse, DEĞİL kapısından sonra 1 verme olasılığı daha yüksek hale geldiği anlamına gelir, ve aynısı tersi için de geçerlidir.
DEĞİL kapısı bu şekilde çalışır: \begin{equation} \ket{0} \rightarrow \ket{1} \end{equation} \begin{equation} \ket{1} \rightarrow \ket{0} \end{equation} \begin{equation} \alpha_{0}\ket{0}+\alpha_{1}\ket{1} \rightarrow \alpha_{1}\ket{0}+\alpha_{0}\ket{1} \end{equation}
DEĞİL kapısını bu matris şeklinde yazabiliriz (ayrıca X kapısı veya Pauli X kapısı da denir): \begin{equation} X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \end{equation}
Nasıl çalıştığını anlamak için bu matrisi bu üç farklı durumla çarpmayı deneyin: \begin{equation} \begin{bmatrix} 0 \\ 1 \end{bmatrix} , \begin{bmatrix} 1 \\ 0 \end{bmatrix} , \begin{bmatrix} \alpha_0 \\ \alpha_1 \end{bmatrix} \end{equation}
Hadamard Kapısı
DEĞİL kapısı gibi tüm kuantum kapılarının klasik karşılıkları yoktur - aslında, bir çoğunun yoktur. Hadamard kapısı bu benzersiz kapılardan biridir ve tartışmasız bir şekilde kuantum hesaplamanın en önemli kapılarındandır. Bir çok kuantum algoritması, kübit durumlarını başlatmak için Hadamard kapısına gereksinim duyar. Peki onu özel yapan şey nedir? $\ket{0}$ ya da $\ket{1}$’e uygulandığında, eşit ağırlıklı süperpozisyon oluşturur.
Tanıdık geldi mi? Tıpkı Bıyıkkent bilyelerinin, kırmızı ve mavinin süperpozisyonunda eşit ağırlıklarla başlatılması gibi!
Hadamard kapısı bu şekilde çalışır:
\begin{equation} \ket{0} \rightarrow \frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1} \end{equation} \begin{equation} \ket{1} \rightarrow \frac{1}{\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1} \end{equation} \begin{equation} \frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1} \rightarrow \ket{0} \end{equation} \begin{equation} \frac{1}{\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1} \rightarrow \ket{1} \end{equation}
Bu $\frac{1}{\sqrt{2}}$ değerleri, ölçümde 0 veya 1 gelme şansının yüzde 50-50 olduğu anlamına gelir. Bazen eksi işareti de görebilirsiniz. Bu, olasılıkları değiştirmese de, faz denilen ve gelecek bölümlerde inceleyeceğimiz bir şey oluşturur. Bilyelerimize özel bir tür dönüş(spin) vermek gibidir.
Hadamard kapısının matris gösterimi bu şekildedir: \begin{equation} H = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \end{equation}
Dönüşümlerin nasıl oluştuğunu görmek için matris çarpımlarını kendiniz yapmayı deneyin.
Önemli bir not: eşit ağırlıklı tek-kübit süperpozisyonları kuantum hesaplamada o kadar önemlidir ki kendi özel sembolleri vardır:
\begin{align} \ket{+}=\frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1}\
\ket{-}=\frac{1}{\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1}\
\end{align}
Kübitlerin Geometrik Gösterimleri
Daha görsel ağırlıklı bir matematiksel gösterim tercih ediyorsan, bir kübit durumunun matematiksel gösterimi muhtemelen sana yardımcı olacaktır. Keyfi bir durum $\psi$, sinüs ve cosinüsler ile yazılabilir ki olasılık genlikleri $\alpha_{0} =\cos{\theta}$ ve $\alpha_{1} =\sin{\theta}$ olmak üzere: \begin{equation} \ket{\psi}=\cos{\theta}\ket{0}+\sin{\theta}\ket{1} \end{equation} Bu geçerli bir gösterimdir-unutmayın olasılıkların toplamı her zaman 1 olmalıdır1. \begin{equation} \alpha_{0}^2+\alpha_{1}^2=\cos^2{\theta}+\sin^2{\theta}=1 \end{equation}
Sonuç olarak, keyfi durum $\ket{\psi}$ bir birim çember(yarıçapı 1 olan bir çemberdir) üzerinde şu şekilde gösterilebilir:
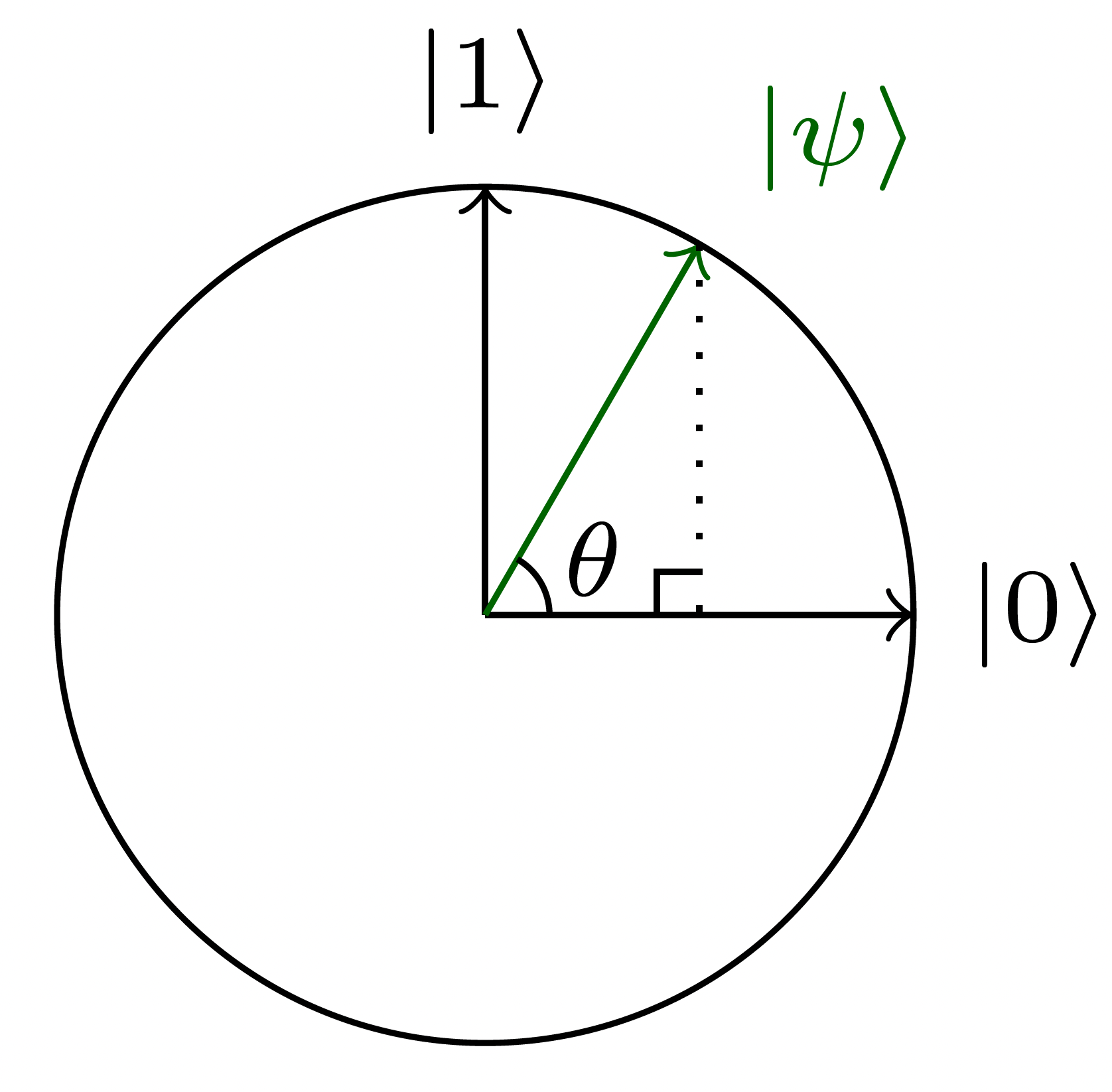
Yeşil vektör keyfi durum, ve iki eksen de baz durumları $\ket{0}$ ve $\ket{1}$’e karşılık gelir.
Eğer $\theta$ açısı 45 dereceyse, $\ket{+}$ durumunu elde edersiniz:
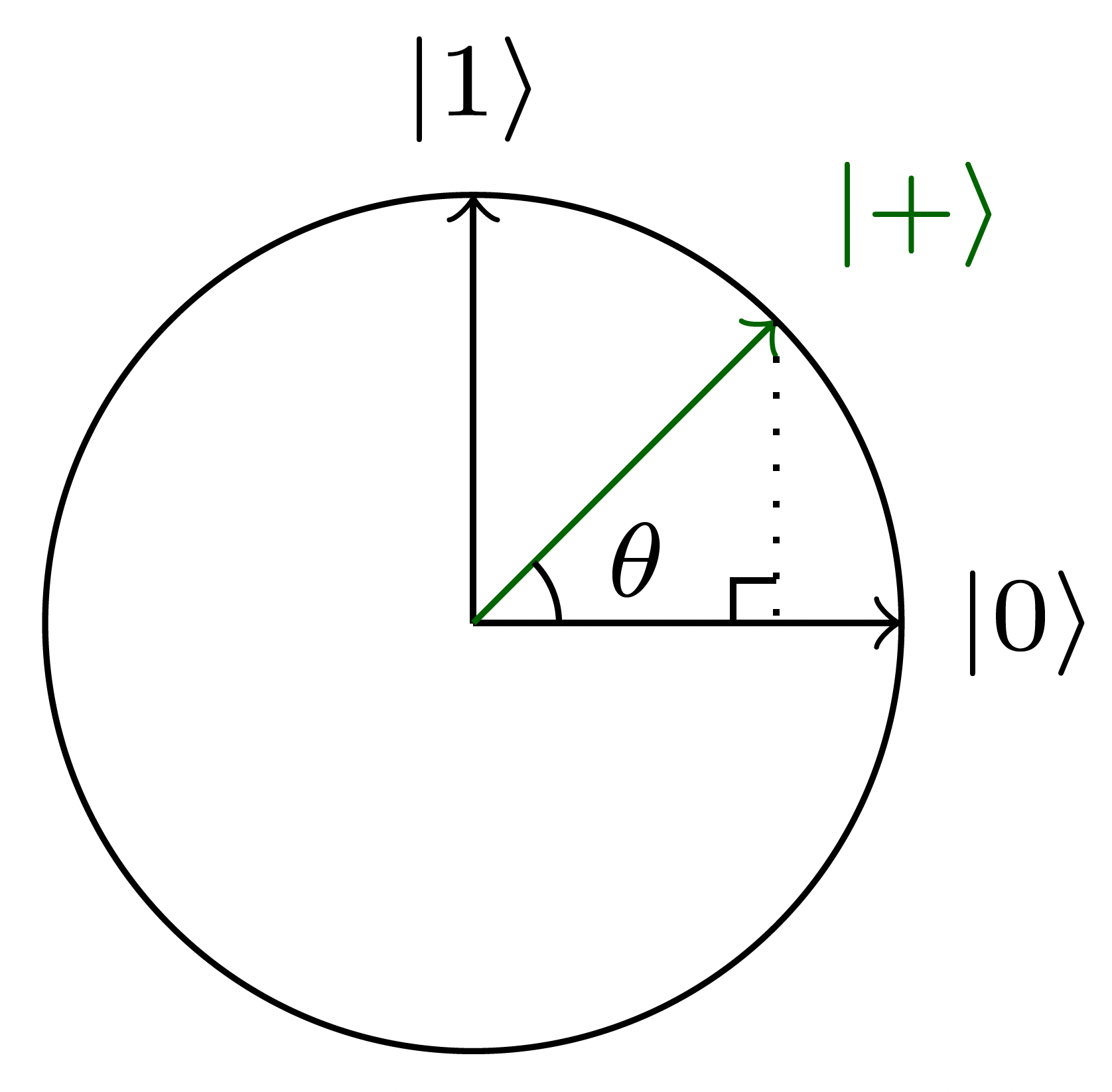
Bu gösterimle, ilgili vektörün $\theta$ açısındaki değişiklere göre çemberdeki hareketleri aracılığıyla bir kuantum kapısının, bir kübit durumu üzerindeki etkisini kolayca anlayabilirsiniz.
Bunun bir kübitin eksiksiz bir gösterimi olmadığını belirtmek önemlidir, çünkü önceden de belirttiğimiz ‘faz’ parametresi burada hesaba katılmamaktadır. Fazı anlattığımızda, Bloch Küresi denilen daha eksiksiz üç boyutlu bir gösterimle karşılaşacaksınız.
Kuantum Devrelerini Çalıştırmak
Artık kuantum kapılarının, kuantum durumundaki olasılıkları manipüle ettiğini anlıyorsunuz. Bu şekilde bir kuantum devresindeki bir dizi kuantum kapısı ya da bir kuantum algoritması, durum olasılıklarını değiştirir. Veya, farklı bir şekilde ifade edecek olursak, kuantum algoritmaları her olası sonuçla ilgili olasılıkları değiştirir.
Doğal olarak merak edebilirsiniz: eğer sonuçlarla ilişkili olasıklar varsa, doğru olmayan ya da istenmeyen bir sonuç elde etme ihtimaliniz yok mudur? Evet, haklısınız!
Bu yüzden, klasik devrelerin aksine, kuantum devrelerini birden çok kez çalıştırır ve sonuçları istatistik olarak toplarız. Devreyi çalıştırdığımız her sefere bir shot denilir ve ne kadar çok shot(atış) yaparsak sonuçlarımız da bir o kadar doğru olur.
Hadi şimdi belirli kapılar uygulandıktan sonra ölçüldüğünde, 0 verme olasılığı %4 olan ve 1 verme olasılığı %96 olan tek kübitlik bir devreye göz atalım:
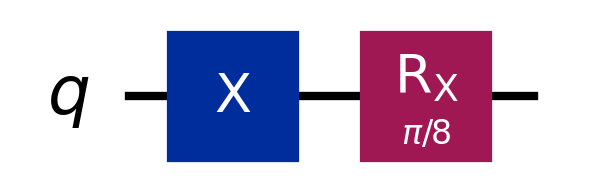
Bu, yukarıda gösterilen X kapısını ve $\frac{\pi}{8}$ açısıyla Rotasyon X ($R_X$) kapısı denilen başka bir kapıyı kullanır. 2
1 sonucunu elde etme olasılığımız göz önüne alındığında, eğer 0’ı maviyle ve 1’i kırmızı ile eşleştirirsek, Luna’nın Mutlu Yıllar şarkısını çaldığı olası kuantum devrelerinden birine sahip oluruz-hatırlayın, bilyeyi gözlemlendikten sonra kırmızı olma ihtimalini yükseltecek şekilde manipüle etmişti.
Bölüm 4 hakkında kısa bir uyarı: Eğer 10 cm mesafe kuralını merak ediyorsanız, bu yalnızca kuantum ölçümleri için kullanılan tuhaf bir hikaye anlatım aracıdır. Gerçekte kuantum ölçümleri, kuantum durumlarının temel durumlarından birine yerleşmesine neden olan fiziksel etkileşimler aracılığıyla gerçekleşir. Kuantum ölçümlerinin açıklaması için Bölüm 2‘ye bakınız.
Qiskit Kodu
Eğer daha öncesinde bu bölümdeki kuantum kapıları ve devrelerine aşina değilseniz, ve Qiskit ile kodlamayı denemek isterseniz, devreleri kodlamak için Bölüm 2 Kısım 2 ve Bölüm 3 Kısım 2‘deki Qiskit bölümlerine geri dönebilirsiniz.
Aksi halde, egzersiz olarak Luna’nın Mutlu Yıllar devresini kodlamaya çalışın!
